Learning new skills often keeps me away from that guy.

Pickhardt-Richter payments are now merged into core-lightning

https://github.com/ElementsProject/lightning/pull/6376

Yesterday evening a person ask me:

"If bitcoin keys are generated randomly by the software,

isn't there a probability that two different people can generate the same

private key?"

This probability is astronomically small and we can compute it approximately.

To solve this we need to take into account that there are N = 2^256 = 10^77

possible private keys, but what we should look is the space of bitcoin addresses,

because to spend a P2PKH or P2WPKH output it suffices to have a

private key that produces the

same public key hash in the transaction output, ie. some private key that

produces a specific bitcoin address.

Since bitcoin addresses are computed from RIPEMD160 hashes, this means that the

space of bitcoin address is M=2^160=10^48.

If we consider x=10^10 people (8 billion at the time of writing)

in the world would generate y=10^6 addresses in their lifetime;

to put into perspective there are 800000 hours

in the lifetime of a 100 year old person.

Then the probability of no collision at all

is the number of possible ways to hit different addresses in the address space:

M (M-1) (M-2) ... (M-xy+1) = M! / (M-xy)!

divided by the number of possible choices:

M^(xy)

hence the probability of no collisions is

prob0 = M! / (M-xy)! / M^{xy}

since M!/(M-xy)! is approximately

M^{xy} - (1+2+...+xy) M^{xy-1} = M^{xy} - (xy)^2 /2 M^{xy-1}

we have

prob0 = 1 - (xy)^2 / 2 / M

Now, the probability of having at least one collision is prob1 = 1-prob0

which for large numbers at leading order becomes

prob1 = (xy)^2 / 2 / M

The square in the numerator the responsible for the so called

birthday paradox, ie. in a group of 20 people the chances of a birthday

collision is very high because 20^2/2 = 200 which is comparable to the number of

days in the year.

The collisions in the case of bitcoin are so unlikely because (xy)^2 = 10^32

while M=10^48 so that

prob1 = 1/10^16 = 0.000 000 000 000 000 1

not as small as the probability of a private key collission but still very

unlikely.

We accept MasterCard but only after you have properly registered with full name, date of birth, email address, telephone number, home address. You must upload a recent utility bill to proof your identity and address.

My Pull Request for Pickhardt payments implementation in core-lightning has passed all CI tests.

I'll zap some sats if you had a lightning address. Great contents!

how much did you pay today in LN fees?

Ordinals and BRC-20s are flooding the mempool. Whoever is behind this is currently throwing 5 btc per block to miners. To keep it up they'll spend 720 btc a day. I wonder how many Bitcoin do they own. Maybe someone with on-chain analysis skills could estimate this based on the addresses being used so far to pay for the attack.

Hi. Do you do the chain analysis on your own? I would like to learn how to do this stuff with my node.

max HTLC, ..., let me check. Thanks a lot!

this is amazing. I run a small node myself, but I earn just like 50 sats/month. How much liquidity approx. do you invest in your node ?

I suggest to follow nostr:npub13lkyycj8s3da6fhndtj0wd6s3s2ahmq86s7wrruvzd4tnc66cgfqn4lpsy, for information about the environmental impact of Bitcoin. nostr:npub16y8hrxftlevzj7yf98l9yvvt2sytke9rcf2ytfucqxy2r59zk8hqwdfdmv

nostr:nevent1qqstfj5k8qmsmtg660jtryapu26xgtnjxw8httgc6uv8r956mwgpjjgpz3mhxue69uhhyetvv9ujumn0wd68ytnzvupzpl3nw0jkjqwu6s0p60q9342pkae0uqeeltnrc2ftwf2apj70h03qqvzqqqqqqy27fqdt

I also like the landscape photos.

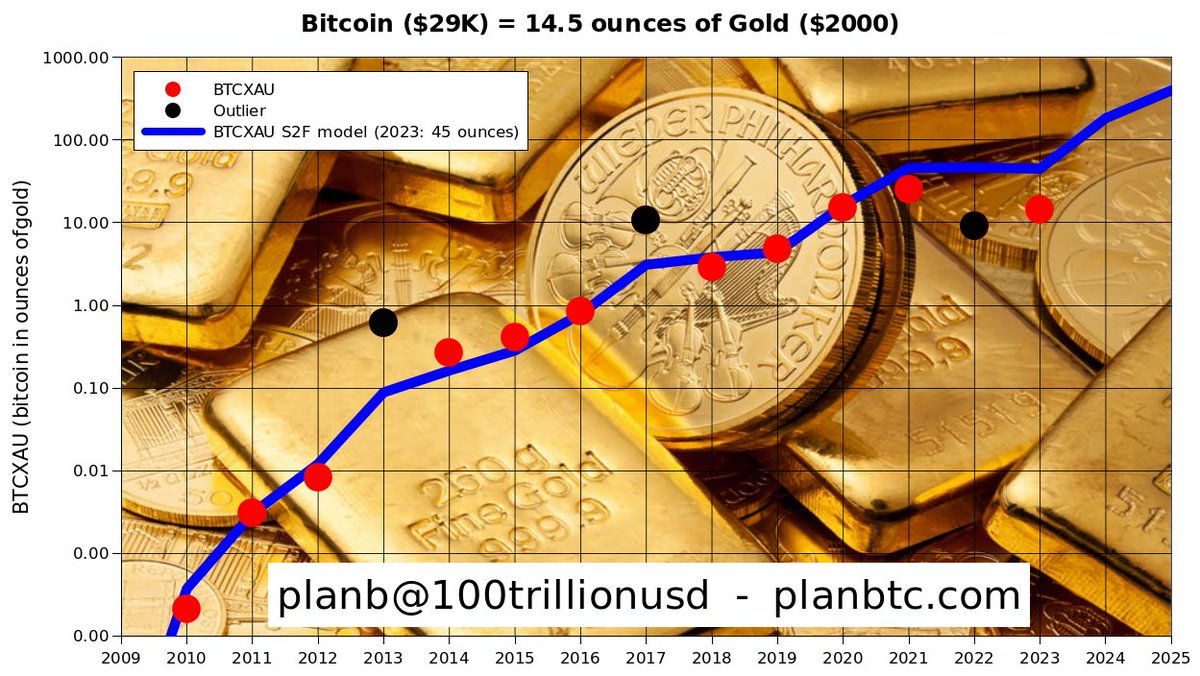
what are the linear coefficients of the fit? With USD you had ln(mcap)=3.3 ln(SF)+14.6

I suspect that the changing SF of USD itself and it's artificial demand by US geopolitics introduces systematics in your fit. Gold, on the other hand has an almost const. SF and demand should also be almost const.

Why so few points? The curve with respect to USD had more data.

Maybe Argentinians should start denominating their products in Bitcoin. (Unit of account)

What if we could host #nostr relays over tor?

Can anyone please tell me what the 13% means. #[0]

, #[1]

ACINQ's Phoenix is a nice self custodial wallet.