2013年3月5号下午,御用摄影师张峻,在雷锋精神宣讲台上讲雷锋的事迹。 讲演结束时,他说:“如果我说的有一句假话,就死在这儿。 说完这句话后,他死在了讲台上! 人在做,天在看。谁说没有报应? https://t.co/GDM02qOEOA 
用生命揭露真相的勇士…
事实核查短文把台湾不属于中华人民共和国的道理讲得很明白。这篇短文隐含着一个事实陈述:海峡两岸一边一国互不隶属。
即中华民国政府自1949年即在台湾独立行使政府管辖治理权力已经长达74年多,判定是否为国家的三要素(有说四要素)完整,事实上是一个国家。中共国与台湾的关系,是国与国之间关系。 https://t.co/yaag6m8bRG 



实际上是在49年之前,台湾地区就已经在行政上隶属于中华民国了,49年只是中华民国失去了对大陆地区的实际治理…
Let's take an example
you have 12 seed words in the following order:
anger animal check effort eight episode just oppose pig possible question sea
By the way, this happens to be one set of possible solutions to your challenge.
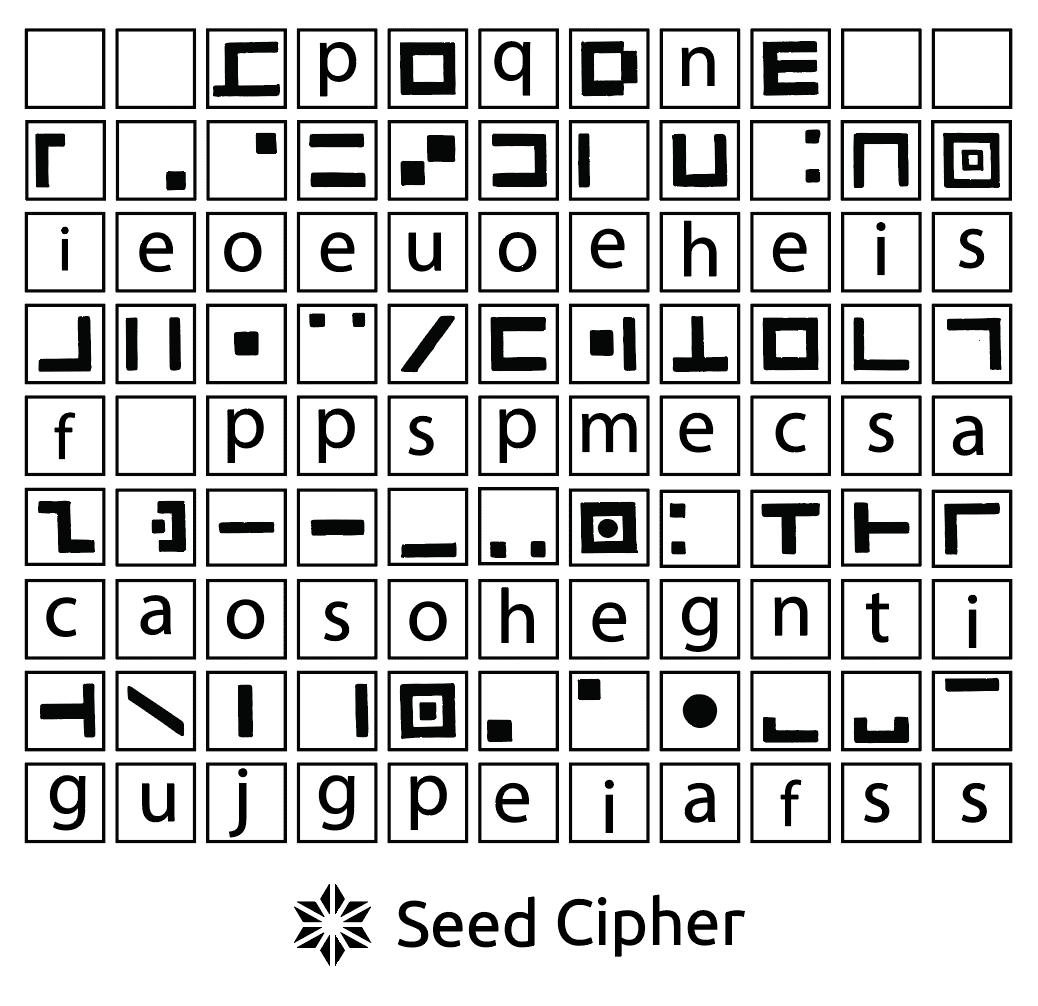
I re-encrypted them with my password card as below

to get the following strings:
h+ike2Tk2hK9!%%+%@7#S9fVhMV^pVMV!h9Tb=2S9&Xe+hs8~npf5eMss
I can write this string of characters on a piece of paper and put it anywhere in the public domain, along with my password card.
If no one else knows the plaintext and substitution rules, then your seed words are safe.
And even you yourself know the plaintext of the 12 words, and you know the ciphertext, and you have this substitution table from my password card, but you still can't backtrack my substitution RULES.
Once you can do that, guess my substitution rules, you can restore another ciphertexts that I have written on paper and made public:
5hK9!spT&=h+Vs%9K9bXh+hY7fM2&8%+X@e9M2fVhMXspVT^h%Ss@2h+XP
You'll find this is another group of MY seed words:
XXXXXX XXXXXXX XXXXXXX XXXXXX XXX XXXXX XXXXX XXX XXXXXX XXXXX XXXXXX XXXXXXXX
By the way, this group of seed words is another set of possible solutions to your challenge.
can you make it?
As you can see, the key to security becomes the RULES, and it's always easier to memorize the rules than it is to memorize individual ciphers one by one, so I use this card to manage all of my high-strength passwords over 8 years, and I'm sure it can be used to keep the seed words safe as well.
In simple terms, the ciphertext and substitution table are publicly displayed, and without knowing the rules, it is impossible to reverse deduce the plaintext. Even if the plaintext, ciphertext, and substitution table are publicly displayed, it is impossible to reverse deduce the rules. I will give an example to illustrate this later.
nostr:npub10wcdqdy9950akm8vzxugg6pqma4x7w6flvfepzdf062fxny2un0qxah257 has been working on brute forcing this and has made it pretty far actually which is crazy
Brute force is not feasible for this problem. With the current global computing power, brute force can significantly reduce the search range, but it is still not small enough for luck to play a role in a meaningful time.
In fact, the whole method should be put on fire, not just the most secure part. You can send me these 12 seed words in the correct order in a private message, and I will encrypt them using a public substitution table and send the ciphertext back to you. If you already know the plaintext and the ciphertext, and the table, try to reverse the encryption rules.
no, this challenge is to restore the private key from random characters, which is the security foundation of Bitcoin and cannot be challenged
In fact, the painting gives clues to restore the 12 seed words in the correct order, as the author said, this is a simple substitution cypher, it is impossible to restore it by just have the seed plate, and you can't even start guessing with just the painting, only by putting the seed plate and the painting together can you solve the private key.
And as I told the author, the password management tool I have actually used for the past 8 years can also be used for seed word encryption, which allows to publish seed plate and painting at the same time and still be unbreakable
there are too many collisions with just 46 letters, you need to reveal corresponding painting to narrow down the scope
制度性的恶,是吃什么不吃什么的问题吗?有那工夫列黑名单,为什么不离开那种屎坑?
I don't think this information is helpful, in other words, in practice to resist reverse derivation, the attack vectors won't contain this information.
A little guess on it, the 10 letters b, d, k, l, r, v, w, x, y, z do not appear in this character set, therefore, among the 2048 words in BIP-39, cut the first 4 letters out first, and then delete all the words containing these 10 letters, leaving only about 600 candidate words.
On the other hand, to uniquely express 12 seed words, each taking the first 4 letters requires 48 letters. Only 46 are given here. Therefore, there are, and only 2 words that are 3 letters long, and there are 10 words are 4 letters in length.
If this guess is correct, it should be feasible to run a letter counting program for random combinations of 12 words on the compiled 600-length word list, but this may cause collisions, different combinations may produce the same letter count.
FYI.
Basically, I use such a card to manage passwords. Of course, there is no problem in recording the seed words. You can even display the card and the cipher text publicly, and no one can restore the seed words. 
I understand that this is a substitution, but the introduction of 44 new symbols is inconvenient for users.
In fact, I currently use a credit card-sized metal card, with a one-to-many substitution table on the card face, and then switch the substitution set through the rules I define, as long as the rules are kept secret, your plaintext will be safe no matter the ciphertext is displayed publicly, or the card face and ciphertext are displayed at the same time. FYI.