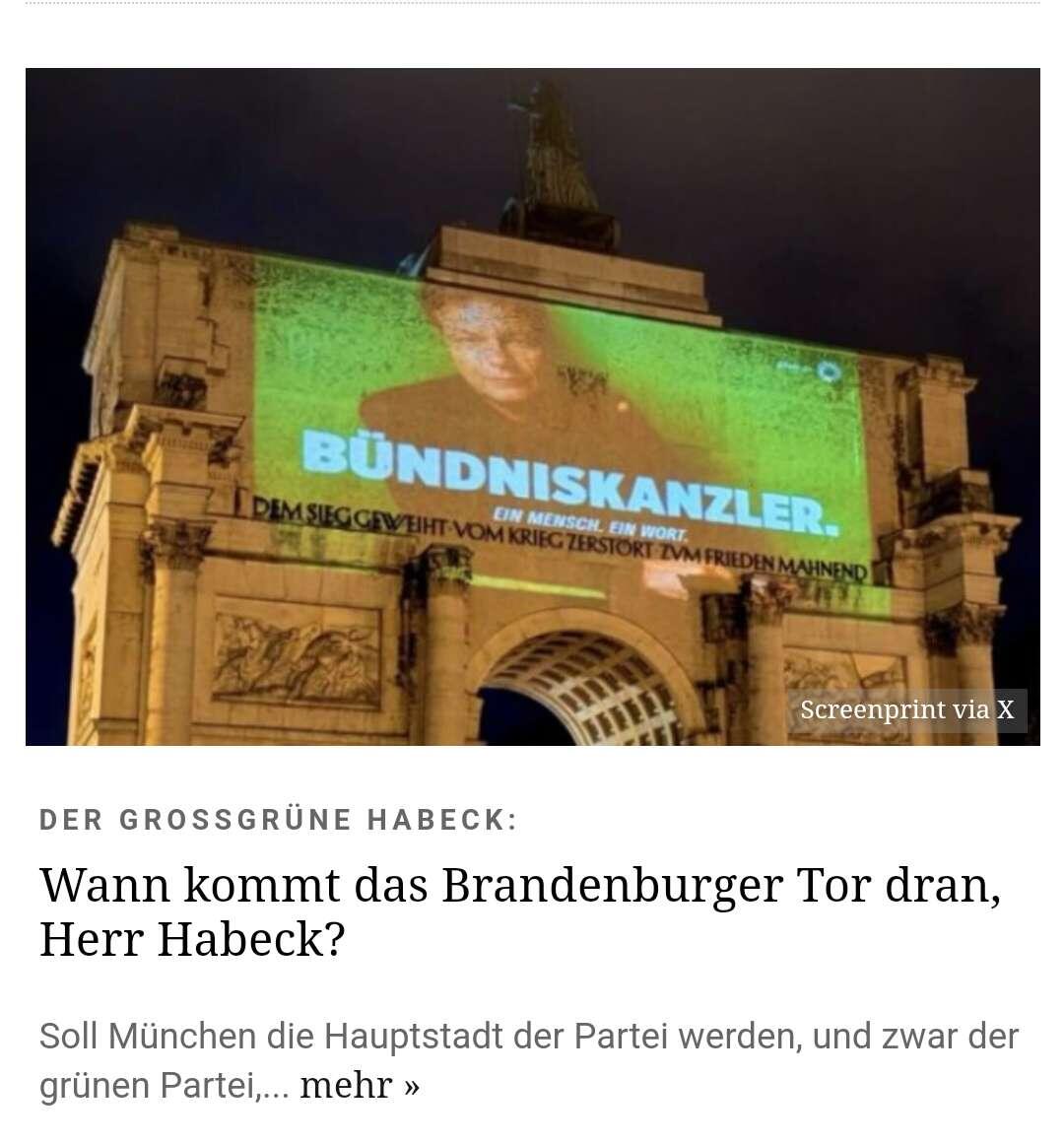
Er hat es überhaupt nicht nötig so zu agieren. Es kommt sehr unseriös rüber. Bin gespannt ob er die Kritik bei X angenommen hat.
Good Morning ☕️ ⛅️ 🌊 you wonderful Nostr people 🫂 💜
Bitcoin fixes this 👇🏻
#Bitcoin #Coffeechain https://video.nostr.build/1981eae41ecaf4e1bec513055fd6c72fe691de724f27ea36f00a9ae967f634a4.mp4 
Also was der Marc so veröffentlicht, seitdem er nach El Salvador ausgewandert ist … 🙈
Die gleiche Clickbaits Masche wie es die Dubai 🤡 tun.
Größenwahn +
Selbstüberschätzung +
Selbstdarsteller + Meinungen anderer strafrechtlich Verfolgen =
January 6, 2021. 😉
#Capitol #Trump 🗽 https://video.nostr.build/0bb3bf1c6e6a56d7cddd75c7e58665a6e4ca90ac7dfa2b3f41368f595c12ab05.mp4 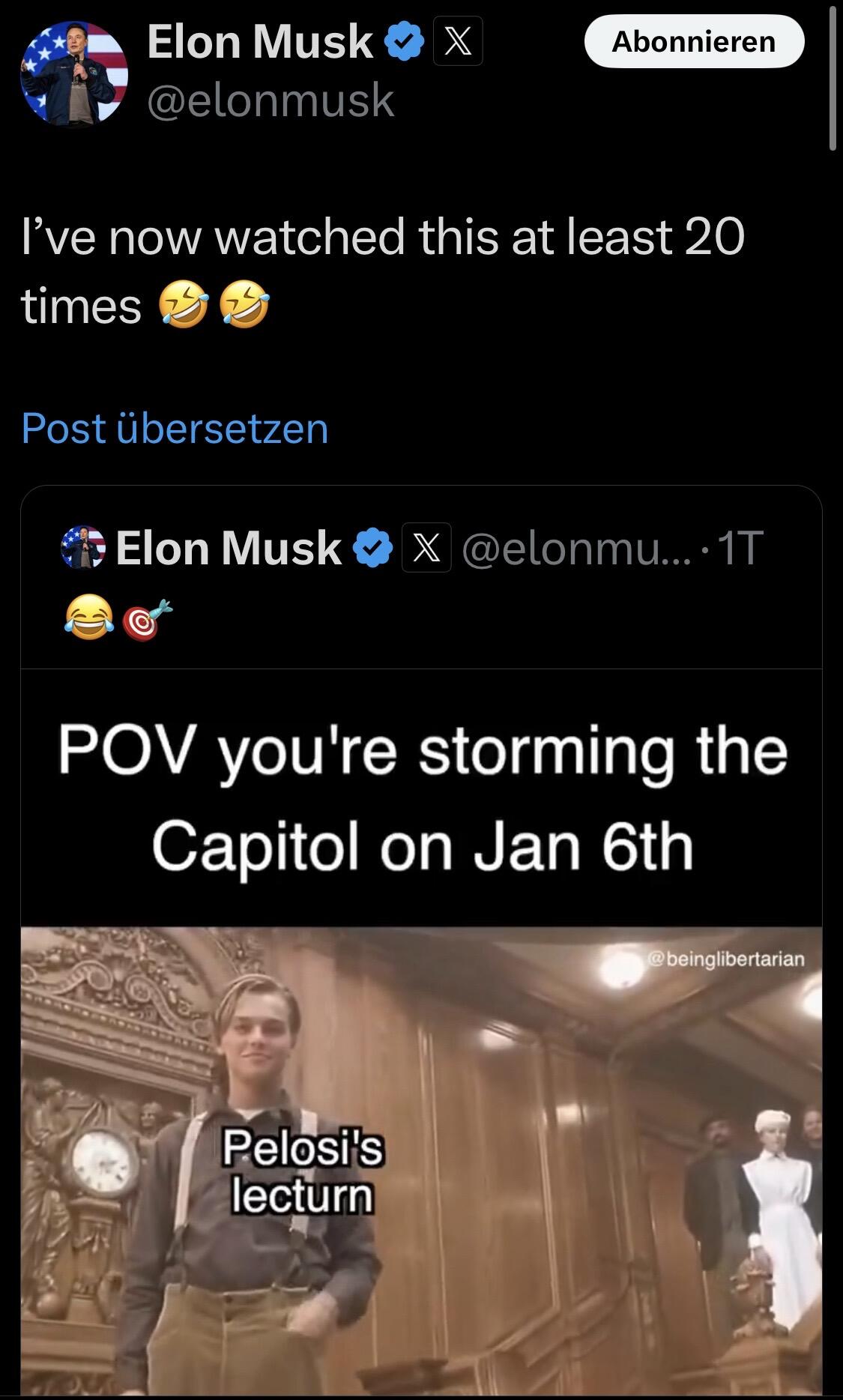
Heute um 19:15 Uhr, sprechen bullishe Bitcoiner live über die aktuellen Geschehnisse rund um Bitcoin und Einundzwanzig.
#Bitcoin #Einundzwanzig nostr:npub1qv02xpsc3lhxxx5x7xswf88w3u7kykft9ea7t78tz7ywxf7mxs9qrxujnc mit nostr:npub1yv72w6v2qqex9r8zh2fftyesfq0g6xegz5ugsy8p0spmfw4z5u7sm3fjqg und #DerPraxmathiker
Fugi mal wieder in Bestform 👌🏻 und genau auf den Punkt gebracht 💯
#FinanzmarktWelt
#GrüneSekte #KlimaLüge
https://youtu.be/E9HqmftNecs https://video.nostr.build/0509c9e6cd134190980e097b5e9ba1c2a88785418e1d8fe8964d32ca733ec923.mp4
Good Morning ☕️ ⛅️ 🌊 you wonderful Nostr people 🫂 💜
#Bitcoin #Coffeechain https://video.nostr.build/88acf8b6f2f49fa1c22af9ca10afbc290efde3faa139d398f76d7a8dc6094513.mp4 
#Meme #Memes #Memestr #Bitcoin 
Sent from my #Bindle
-> follow nostr:npub1u3vyr0ym09vynsntyq873ujusseu4zdku2p7r0jggkxedav9m3fscmxdn6
#plebchain #einundzwanzig #bitcoin #nostrplebs #artstr

😂👌🏻
Good Morning ☕️ ⛅️ 🌊 you wonderful Nostr people 🫂 💜
#Bitcoin #Coffeechain
#BalticSea https://video.nostr.build/c9ec1b95d6d6b7bd5c9635af5558abab8d896025c77721a7d2324751afa54a64.mp4