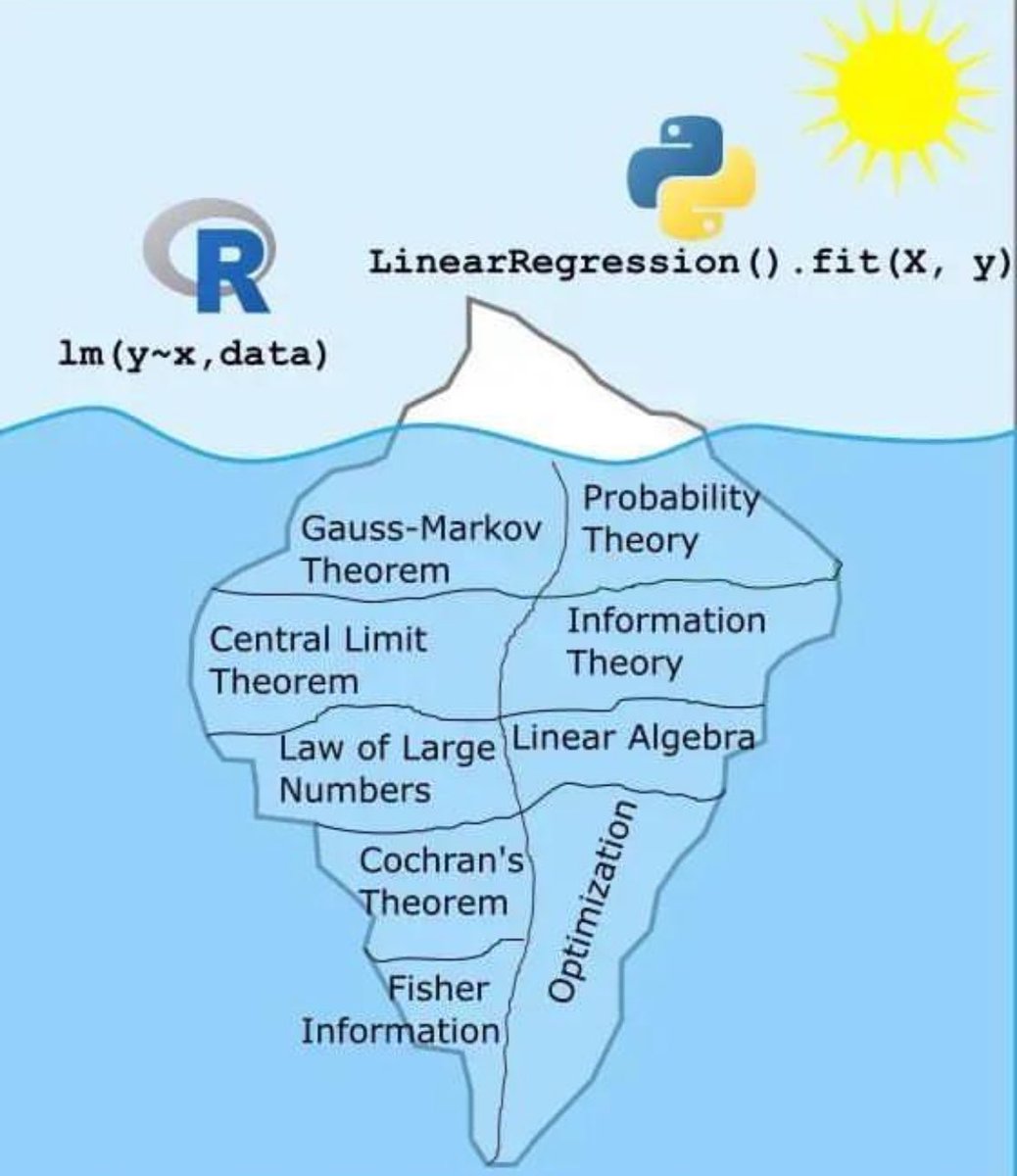
线性回归冰山图：背后隐藏的数学和统计知识

这张图用冰山的形象生动地展示了线性回归模型的表面操作与其背后复杂的数学和统计理论之间的关系。我们平时在R语言和Python中使用简单的一行代码来进行线性回归，但实际上，这一行代码背后有很多深奥的理论支持。

冰山上的部分（表面）

- R语言：`lm(y~x, data)`

- Python：`LinearRegression().fit(X, y)`

这些是我们在编程中常用的命令，用来快速实现线性回归。这部分就像冰山露出水面的部分，简单明了。

冰山下的部分（隐藏）

1. 高斯-马尔可夫定理（Gauss-Markov Theorem）：确保在线性回归中，最小二乘估计具有最佳线性无偏估计（BLUE）的性质。

2. 中心极限定理（Central Limit Theorem）：说明在样本量足够大的情况下，样本均值服从正态分布，这是许多统计推断方法的基础。

3. 大数法则（Law of Large Numbers）：表示随着样本数量增加，样本均值会接近总体均值。

4. 科克伦定理（Cochran's Theorem）：用于分析方差分解的重要理论。

5. 费舍尔信息量（Fisher Information）：用于衡量参数估计中的信息量和精确度。

6. 概率论（Probability Theory）：提供了处理随机事件和不确定性的基础理论。

7. 信息论（Information Theory）：帮助理解数据中的信息量及其传递方式。

8. 线性代数（Linear Algebra）：在线性回归中用于处理矩阵运算，如求解系数向量。

9. 优化理论（Optimization Theory）：在线性回归中用于找到最佳参数，使得误差最小化。

总结

通过这张图，我们可以看到，虽然实现线性回归的代码非常简洁，但其背后依赖的是大量复杂而深奥的数学和统计学理论。这些理论共同支撑了我们所看到的简洁而高效的模型应用。