每日一题 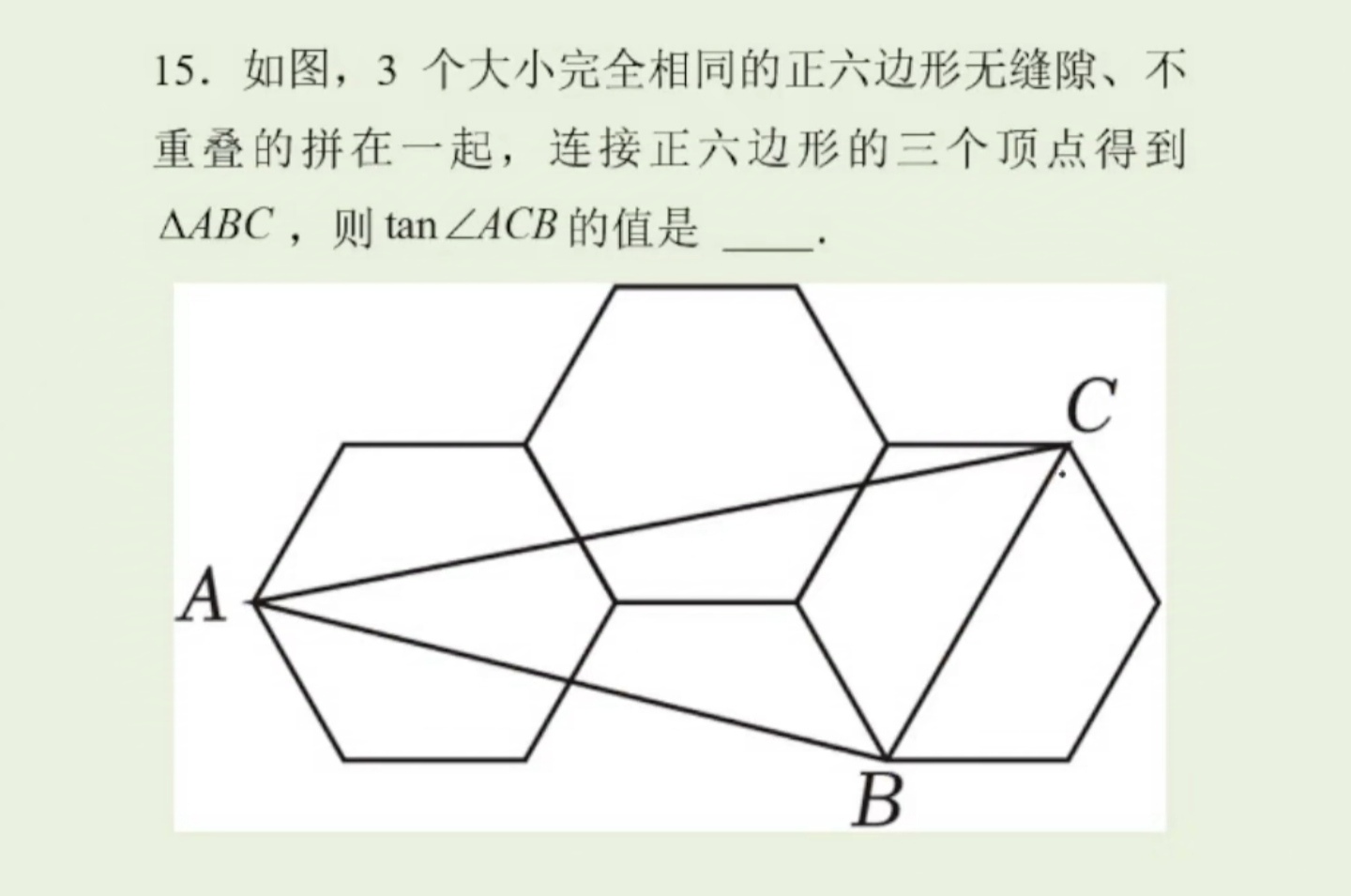
Discussion
来自“豆包”的解答
1. 首先,观察图形可知,正六边形的内角为120^{\circ}。
- 因为\angle BAC = 120^{\circ},\angle ABC = 120^{\circ}。
2. 然后,在\triangle ABC中,\angle ACB = 180^{\circ}-\angle BAC-\angle ABC。
- 所以\angle ACB = 180^{\circ}-120^{\circ}-120^{\circ}=-60^{\circ},这显然不对,说明我们需要重新思考。
- 实际上,我们可以通过观察发现\triangle ABC是一个等腰三角形,AB = BC。
3. 接着,我们可以利用正六边形的性质来求\angle ACB。
- 设正六边形的边长为a。
- 由正六边形的性质可知,AC = \sqrt{3}a,AB = BC = a。
4. 最后,利用三角函数来求\tan\angle ACB。
- 在\triangle ABC中,\tan\angle ACB=\frac{AB}{BC}=\frac{a}{a}=1。
所以,\tan\angle ACB的值是1。
文本复制的乱七八糟,还是截图了

再来个kimi的,竟然结果不同



