揭开数据背后的秘密：简单线性回归的奇妙世界！

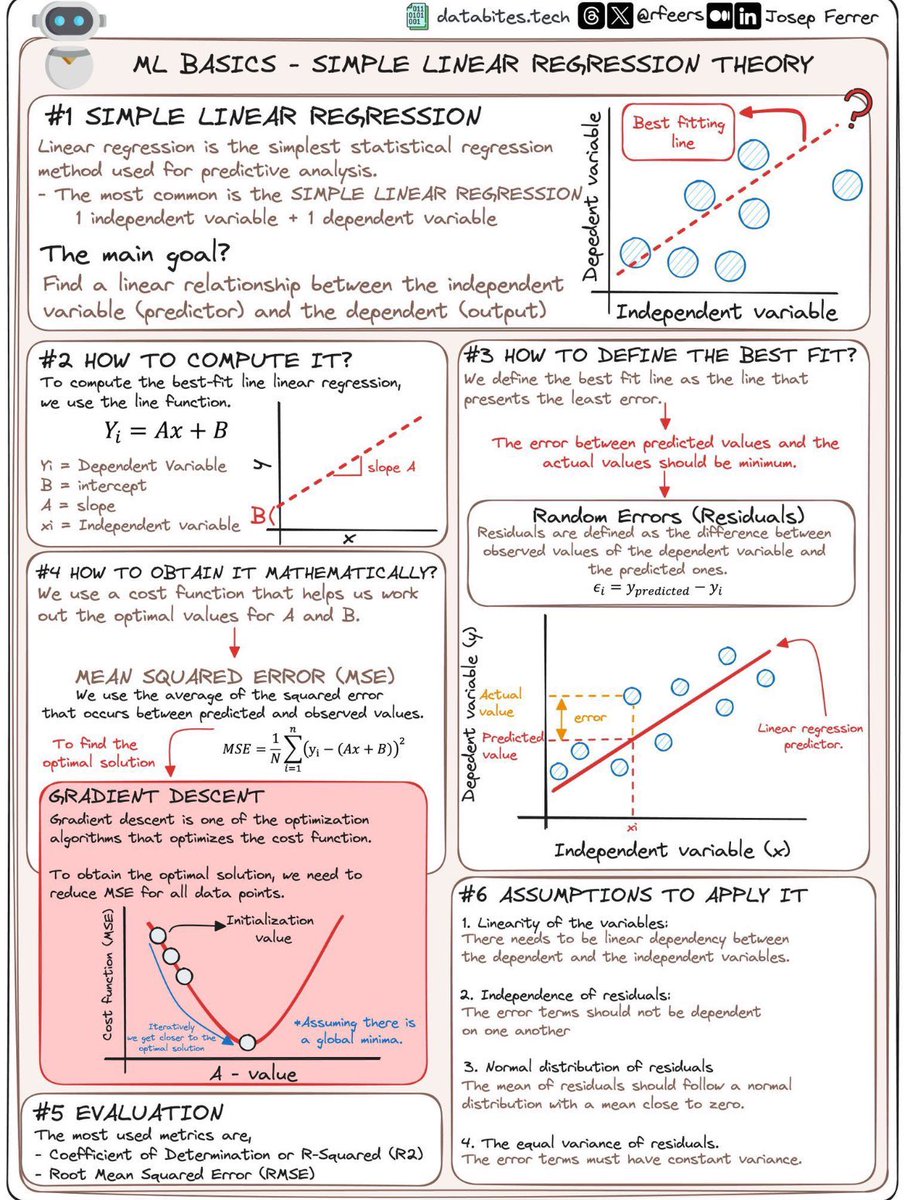
这张图详细介绍了简单线性回归的基本概念和步骤。

1 简单线性回归

- 定义：最简单的统计回归方法，用于预测分析。

- 目标：找到自变量（预测器）和因变量（输出）之间的线性关系。

- 结构：1个自变量和1个因变量。

2 如何计算？

- 使用线性函数计算最佳拟合直线：\( Y_i = Ax + B \)

- \( Y_i \)：因变量

- \( A \)：斜率

- \( B \)：截距

- \( x \)：自变量

3 如何定义最佳拟合？

- 定义为误差最小的直线。

- 随机误差（残差）：观察值与预测值之间的差异。

4 如何数学上获得它？

- 使用损失函数寻找A和B的最优值。

- 均方误差（MSE）用于计算预测值与观察值之间的平均平方误差。

- 梯度下降法：优化算法，降低所有数据点的MSE以获得最佳解。

5 评估

- 常用指标：

- 决定系数或R平方（\( R^2 \)）

- 均方根误差（RMSE）

6 应用假设

1. 变量线性关系：因变量和自变量之间需有线性依赖。

2. 残差独立性：误差项不应相互依赖。

3. 残差正态分布：残差均值应接近零且呈正态分布。

4. 残差等方差：误差项应具有恒定方差。

这张图帮助理解简单线性回归的理论基础、计算方法及其应用条件，非常适合初学者参考。