深入浅出：简单线性回归的核心概念与应用指南

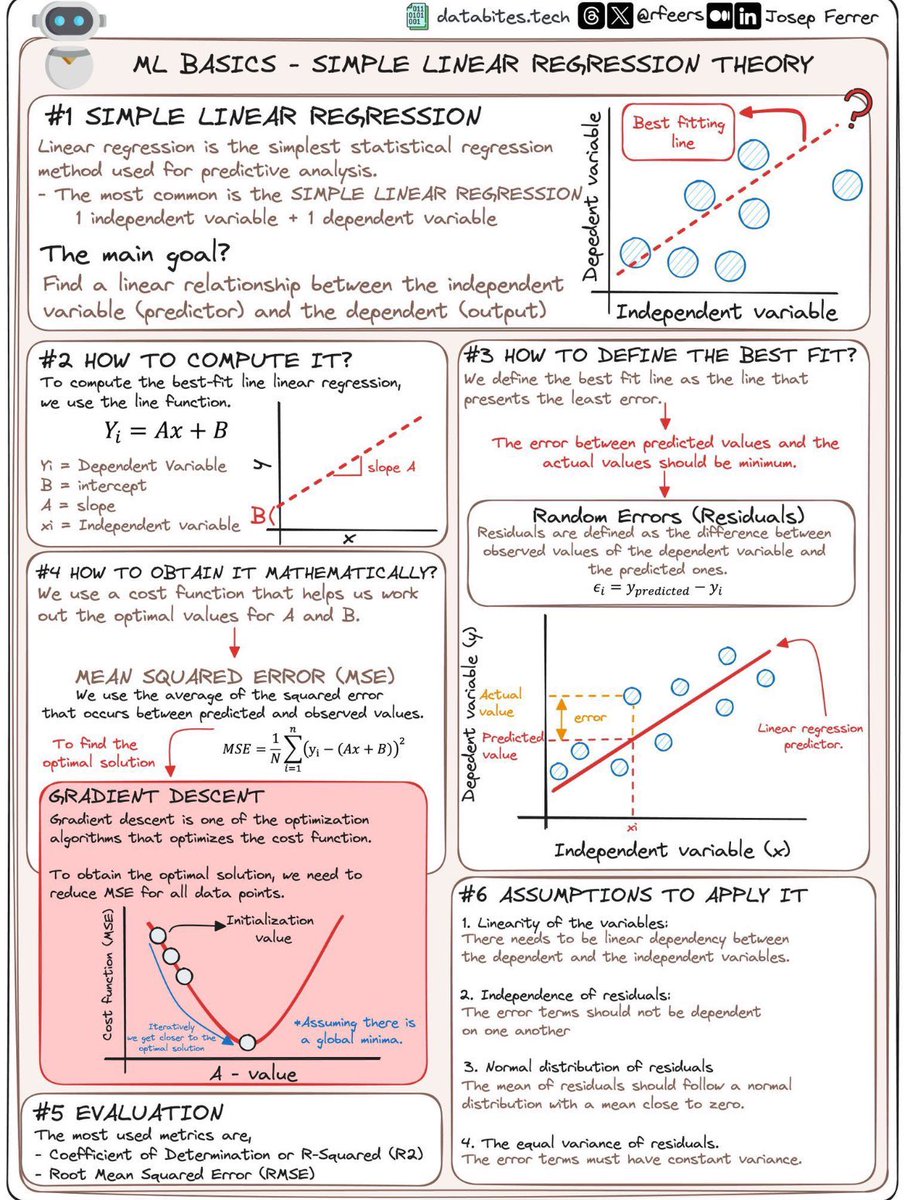
这张图详细讲解了简单线性回归的基本理论及其应用方法。。

主要内容解读：

1. 简单线性回归简介：

- 线性回归是一种常见的统计回归方法，用于预测分析。

- 目标是找到自变量（预测变量）和因变量（输出）之间的线性关系。

2. 计算方法：

- 使用线性方程 \( Y_i = Ax + B \) 来计算最佳拟合直线。

- 其中 \( A \) 是斜率，\( B \) 是截距。

3. 定义最佳拟合：

- 最佳拟合线是使误差最小的那条直线。

- 误差被定义为预测值与实际值之间的差异。

4. 数学求解：

- 使用代价函数（如均方误差，MSE）来寻找 \( A \) 和 \( B \) 的最优值。

- 梯度下降法是一种常用的优化算法，用于最小化代价函数。

5. 模型评估：

- 常用指标包括决定系数（R²）和均方根误差（RMSE）。

6. 应用假设：

- 变量之间需要线性依赖。

- 残差相互独立。

- 残差呈正态分布，平均值接近零。

- 残差具有恒定方差。

通过这些步骤和假设，简单线性回归能够有效地用于数据建模和预测分析。