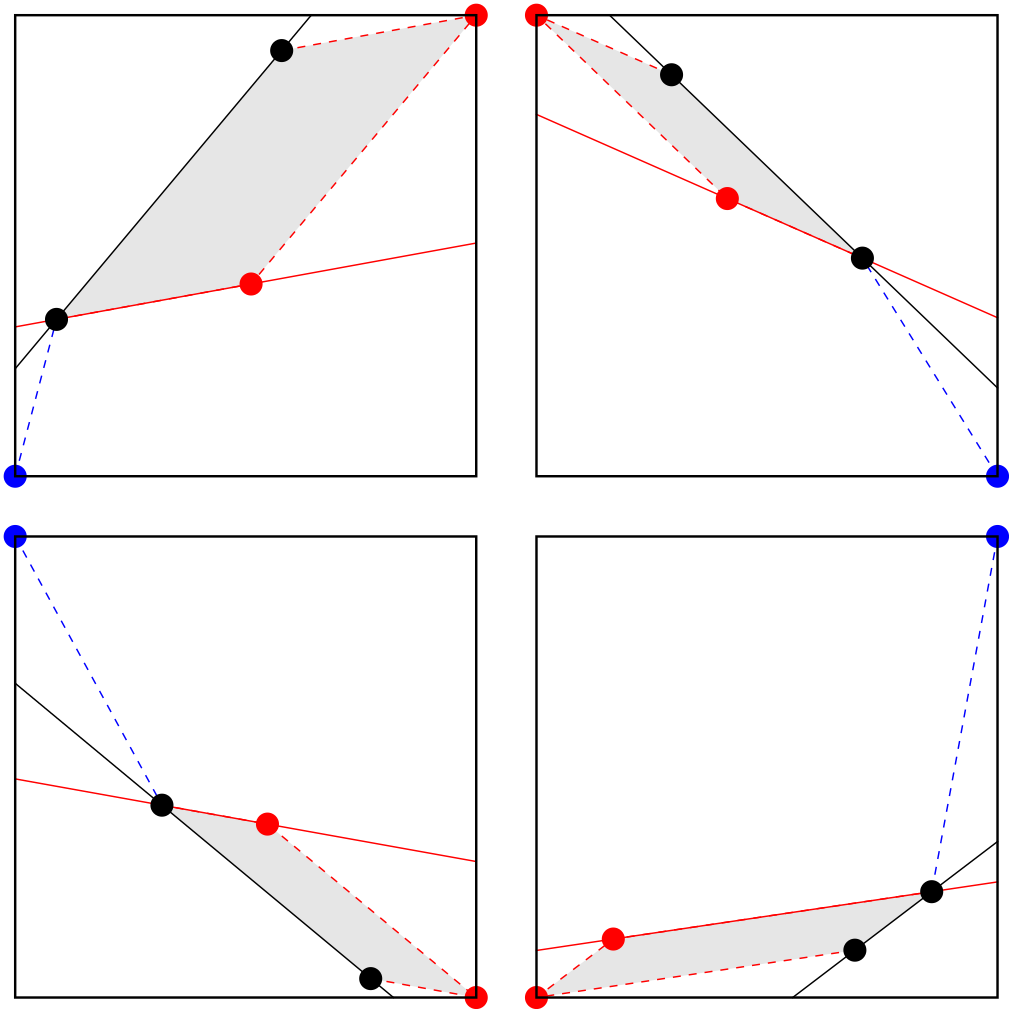
[2/2] What's more, they are all invertible; given a pair of points in that half of Opp, we can always locate the correct red corner, reconstruct the parallelogram, and find the two black dots in Adj. This might seem ambiguous at first; there is another potential corner to use, the blue dot in each panel. How do we know which one is correct? But depending on whether the line we get from our Opp points slopes up or down, we can compare the two candidate lines that join each corner to one of the points, and pick the correct one by its position at the start or end of the counterclockwise arc running between their directions.
So, these maps tells us that:
Vol(Adj) = ½ Vol(Opp)
because by symmetry we know that the two halves of Opp have equal volume.
But together, the two sets comprise the whole unit hypercube of all pairs of points in the square:
Vol(Adj) + Vol(Opp) = 1
It follows that:
Vol(Adj) = 1/3
Vol(Opp) = 2/3