《破解·系列讲座》
很多人(包括我)都发现大语言模型(LLM)好像具有“超能力”。只要你能问出来的问题,它经常都能找到答案,而且很多时候它是对的。
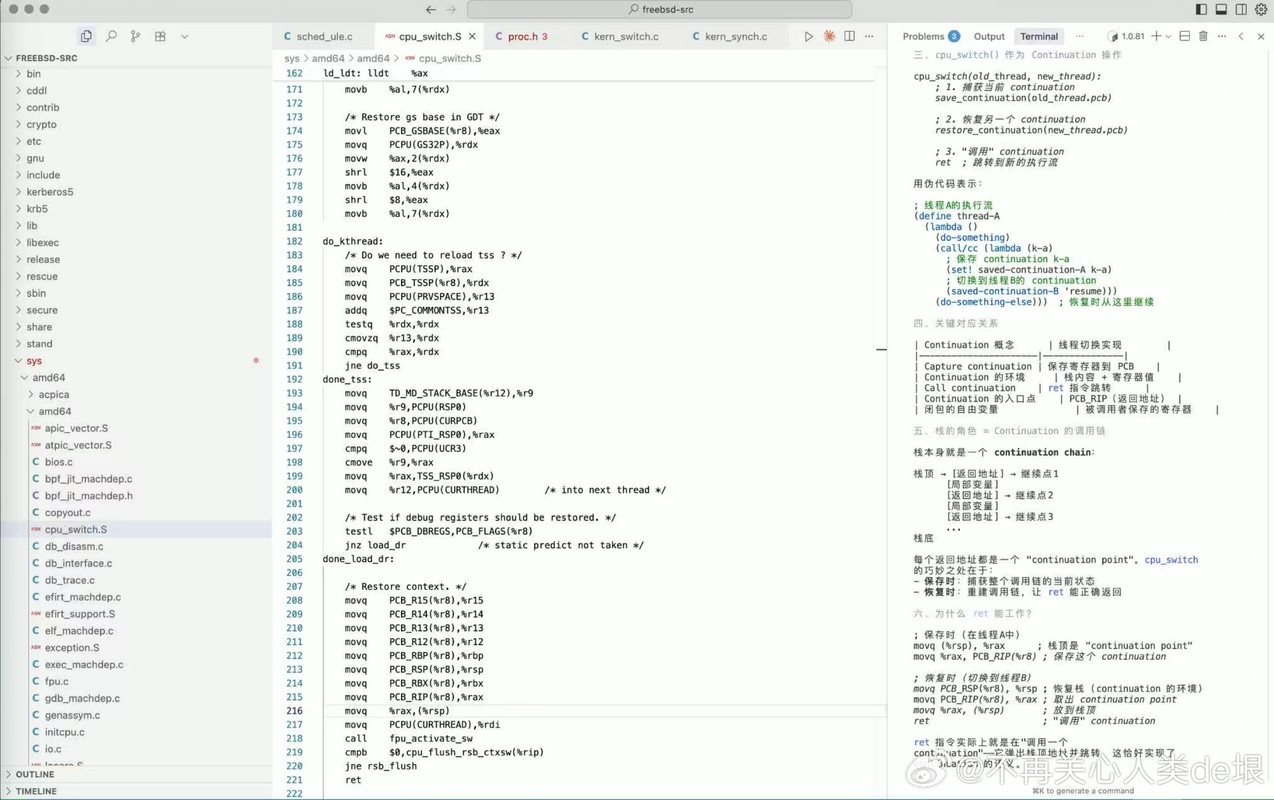
比如,前段时间我问过多个 LLM 这样一个问题(如图),关于操作系统内核的线程切换和 continuation 之间的对应关系。这个问题是2023年“Continuation 专项班”上我向同学们提出来的,却没给他们答案。当时同学们都已经用 continuation 实现了自己的线程切换并发系统,这相当于操作系统内核的最关键部分,但当时我们没有拿现实的操作系统来看。我自己也没去看,最后也没有同学给我回答。毕竟,要拿上千万行的操作系统代码来看,还是比较没有头绪的。
结果前段时间调研 LLM 的时候,我把这问题连同几个操作系统的内核源代码(FreeBSD 和 Linux)交给 LLM,不一会就得到了答案。几乎每个主流 LLM 都能找到这个答案,很精准地定位到汇编语言代码里面,给我解释清楚它是如何对应到带有 continuation 切换的 scheme 代码,让我很是惊讶。这个问题就算是操作系统专家也很难回答,因为操作系统专家并不理解 continuation 的概念,而懂得 continuation 的函数式语言专家却又懒得去看操作系统的 C 和汇编代码。
是不是说 LLM 已经强大到可以取代我了呢?当然不是。LLM 自己能提出这样的问题吗?它们不能。LLM 能很快解决这样的问题,它们却不能提出这样的问题,这真是很有意思。根据最近对 Transformer 模型(LLM 的理论基础)的分析,我发现“不能提出问题”应该是 LLM 的一个本质局限,很可能无法解决。
LLM 不会提出问题,很多人自己也提不出问题。即使勉强提出一个问题,看了 LLM 的回答,他们可能就懵了,也不知怎么提出下一个关键问题。所以虽然有了 LLM,他们仍然无法产生新的发现。
假想一下,如果王垠历尽辛苦,头发掉光之后,成功证明了哥德巴赫猜想,这个猜想会改名叫“王垠定理”吗?当然不。它会改名叫“哥德巴赫定理”,因为这是哥德巴赫提出的问题。王垠没想到这问题,所以虽然他解决了这问题,也不会以他的名字命名,哥德巴赫仍然是比王垠高明的数学家。这就是提出问题的重要性,这重要性比解决问题还高。
能问出好的,关键的问题,这就是一个高明的研究者和其它人的最大差别。我在业界所做出的各种重要成果,创造出教育效果极高计算机科学基础班,进阶班…… 归根结底都离不开这个特征:我首先能提出好的问题,然后我动手去解决这个问题。
我一直以来的苦衷,就是我提出了很多问题,却没有足够的精力去看那些繁琐的技术文献和代码。所以很多问题我还没来得及得到答案。在计算机科学基础班期间,我利用这种有益的压力,解决了很多自己以前没想清楚的问题。可以说,我开班最大的收获不是金钱,而是我从中获得的宝贵信息。这些信息是怎么得到的——上课的时候临场发挥,自问自答!在教学过程中,我学到的东西比我教出去的东西多很多,这就是我为什么喜欢给人上课。😄
现在有了 LLM,情况就很不一样了。我不再需要给人上课来提出并且回答自己的问题。因为我随时想到问题,就输入进 LLM,然后接着问出一系列关键的问题,经常很快就揭晓谜底。
但我个人精力还是有限,很多其它领域我没去看,这仍然限制了我的发挥程度。所以我现在有一个设想,那就是开设一个系列讲座,暂时题名《破解》。这个系列讲座会不定期进行视频(或线下)会议,参加者可以提出自己的困惑,然后我会帮助他调整和精炼问题,利用 LLM 和我的经验,一步步地找到最终答案。这些都是临场发挥,现场演示,跟我上课的方式一样,所以应该会很有意思,能激发很多灵感。
《破解》系列讲座对参加者的背景没有特殊要求。特别欢迎计算机领域以外的其它学科人士,一起探索新大陆。我觉得这是一个很好的互惠互利的活动。对每个参加者,我会收取少量的费用。对于参加过计算机科学班的同学,提供半价优惠。
目前只是一个设想,有兴趣的人可以来信报名 yinwang.advising@icloud.com,题名为“报名《破解》系列讲座”。附带自己的个人说明和微信联系方式。如果足够多的人感兴趣,我们就进行第一次的尝试。