Nostr Web Client

If schizos see everything as being connected, then call me schizo lol.

At this point, I think there may be a lot of false schizo diagnoses (in the serious medical sense of the term).

Years and years ago I heard that mathematicians were more likely than the general population to go schizo.

I'm starting to understand why. The honesty requirement of the wisdom chakra is fulfilled by the mathematician's mindset formed by proofs. Likewise, the same thing happens to scientists whose mindsets are formed by the scientific method.

Not all mathematicians and scientists go this path but it would make sense that a disproportionately large quantity of mathematicians and scientists would "go schizo" in the "everything is connected" sense of the term.

twofish 8mo ago

Yeah I posted about a bit of nuance on this topic.

nostr:nevent1qqsx7gt7cmcmvz2p48dq9jvuq5fykwvfde3ham6dcsnq3fy3l76l4mgpz4mhxue69uhhyetvv9ujuerpd46hxtnfduhsygy7p5azck7lw9smdujgu3d0fq9r6kkeywvy6ux2ggtek5j7yl92hqpsgqqqqqqskw3ls2

In computation a good approach is to determine whether a problem can be reduced or transformed into a simpler or known form. I took some notes about different P vs NP Hard problems and mapping them out. For example, if you have a specific problem, but you can translate the problem to a graph coloring problem, then do that translation, solve it in that domain, and then translate it back. The graph coloring problem is defined here:

https://en.wikipedia.org/wiki/Graph_coloring

Reply to this note

Please Login to reply.

Discussion

twofish 8mo ago

You could argue that the process I lined out in how we solve problems in computation is also described in this picture:

RedTailHawk 8mo ago

This sounds like how I teach trigonometry students how to deal with radians.

I tell them to operate in terms of tau, not pi, then, at the end, convert back to pi if their teacher insists on providing an answer in units of pi.

Tau simplifies things for radians because 1 full revolution is 1 full tau. There is no factor of 2 or 1/2 to deal with...it's just 1:1.

Tau = 2 x Pi

An interesting aspect of Tau is how using it in the circle area formula changes the formula to resemble a pattern found in multiple other places, namely:

y = (1/2) x A x B^2

In this case it's:

Area = (1/2) x Tau x (Radius)^2

Spring energy and kinetic energy formulae both have this pattern. I'm sure there are others.

twofish 8mo ago

And we've gone full circle into Hooke's law 😂👏.

RedTailHawk 8mo ago

Bentov would be so proud. Oscillators and more oscillators…springs and circles.

twofish 8mo ago

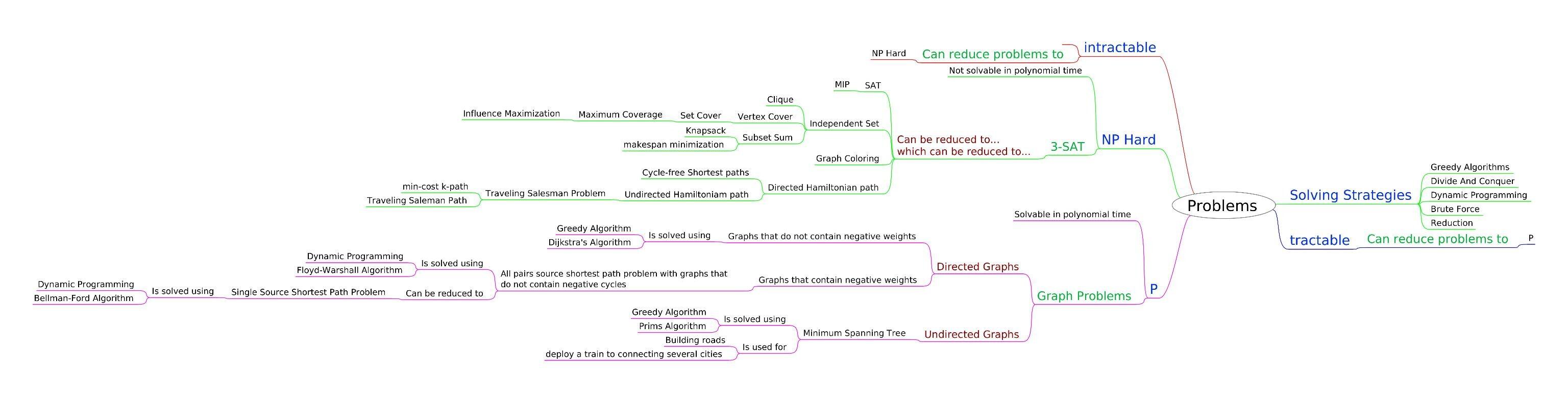
There is also the flip side to this where rather than using reduction or transformation to solve a given problem, we can start with a solution, and come up with applications to which the solution applies. So the solution in abstract form becomes a recipe or blueprint that is easy to understand and you can fill in the variables later.

And then their is an ability to apply a solution to n number of problems, and this is what I am getting at. I think it's called divergent thinking, and I'm not sure what else it is called. Is that just schizo? Seeing how everything is connected?