Replying to Avatar ₿en Wehrman

If you live somewhere where you can see a city, landmass, or landmark VERY far away (10 miles plus, ideally), then you can easily test the heliocentric globe model for yourself. (Binoculars/telescope are encouraged if you have them, so you can see even further; all that matters is that you can establish a visual.)

Once you've made eye contact with Location B from Location A (your location), refer to this chart for the corresponding distance of drop there should be from the curvature of the Earth, according to the official globe measurements.

Do you see the amount of drop that you should?

Report back with your findings!
Avatar
₿en Wehrman 11mo ago

Lil quick test using some PNW landmarks I'm familiar with...

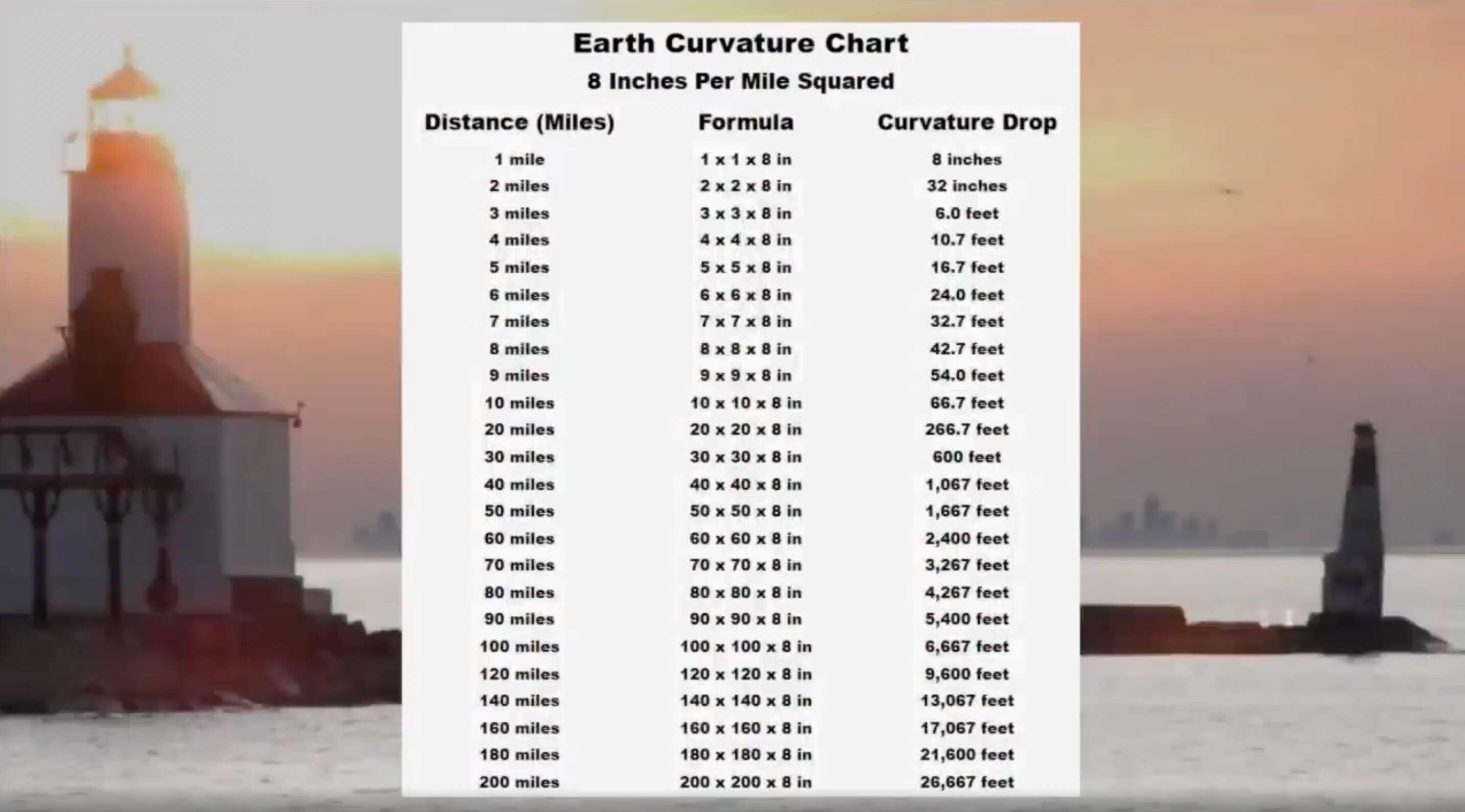
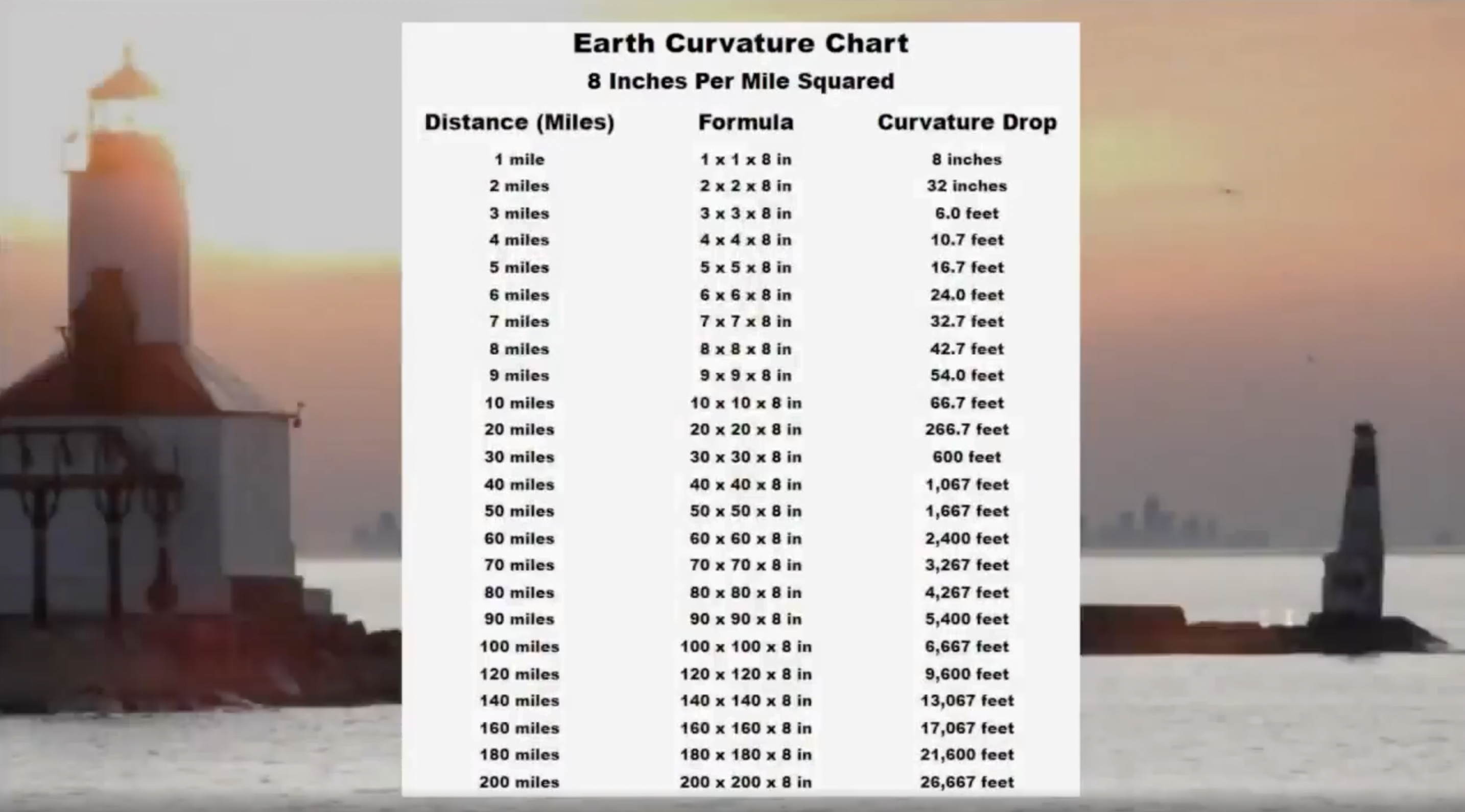
(See reference chart of how much drop in elevation we should see due to earth's curvature over certain ground distances.)

Here's a photo of Mt. Rainier from Vancouver B.C. Almost exactly 200 miles distance, which equal 5.05 miles of drop from curvature.

Tippy top of Mt. Rainier is 2.72 miles in height, so on net, from Vancouver B.C., that peak of the summit should be well hidden 2.33 MILES below ground level from the perspective of the photographer.

Yet you can see the BASE of the mountain, essentially bone-flat with Vancouver despite 200 miles of distance. That's mathematically impossible based on the globe model. #FlatEarth

nostr:nevent1qqsfj30ewvjj6k8ecc5tk2nkl9d33h5fqcwpxsj2cefwztkqk6feqpspz4mhxue69uhhyetvv9ujuerpd46hxtnfduhsygqqrzm7uvlmy5uyxcuuvt3f9lk8qznf4yas3m3hf3da49cunvu4vspsgqqqqqqsnzx3s4

Reply to this note

Please Login to reply.

Discussion

Avatar
Analogue Dog 11mo ago

Looks like you took the pic from halfway up cypress tho.

Avatar
V 11mo ago

big

Avatar
Minz 11mo ago

🤩 Wow!

Avatar
. 2mo ago

This is an interesting idea. It would be most useful to test on smooth open water. It seems that on a perfectly smooth globe one in theory would not be able to see the top of the object extending up above the smooth surface on a globe. I don't know how the equation works when the perspective is from a highly elevated location. This perspective is well above sea level.

Avatar
David Cavan Fraser 2mo ago

Both locations are not at sea level.

Atmospheric Refraction give an extra 10%

Avatar
Dr. Bitcoin, MD 18h ago

Refraction is a thing. A temperature dependent thing.

What you should really ask yourself is why can’t you always see the same amount of the mountain at all time when visibility isn’t limited?