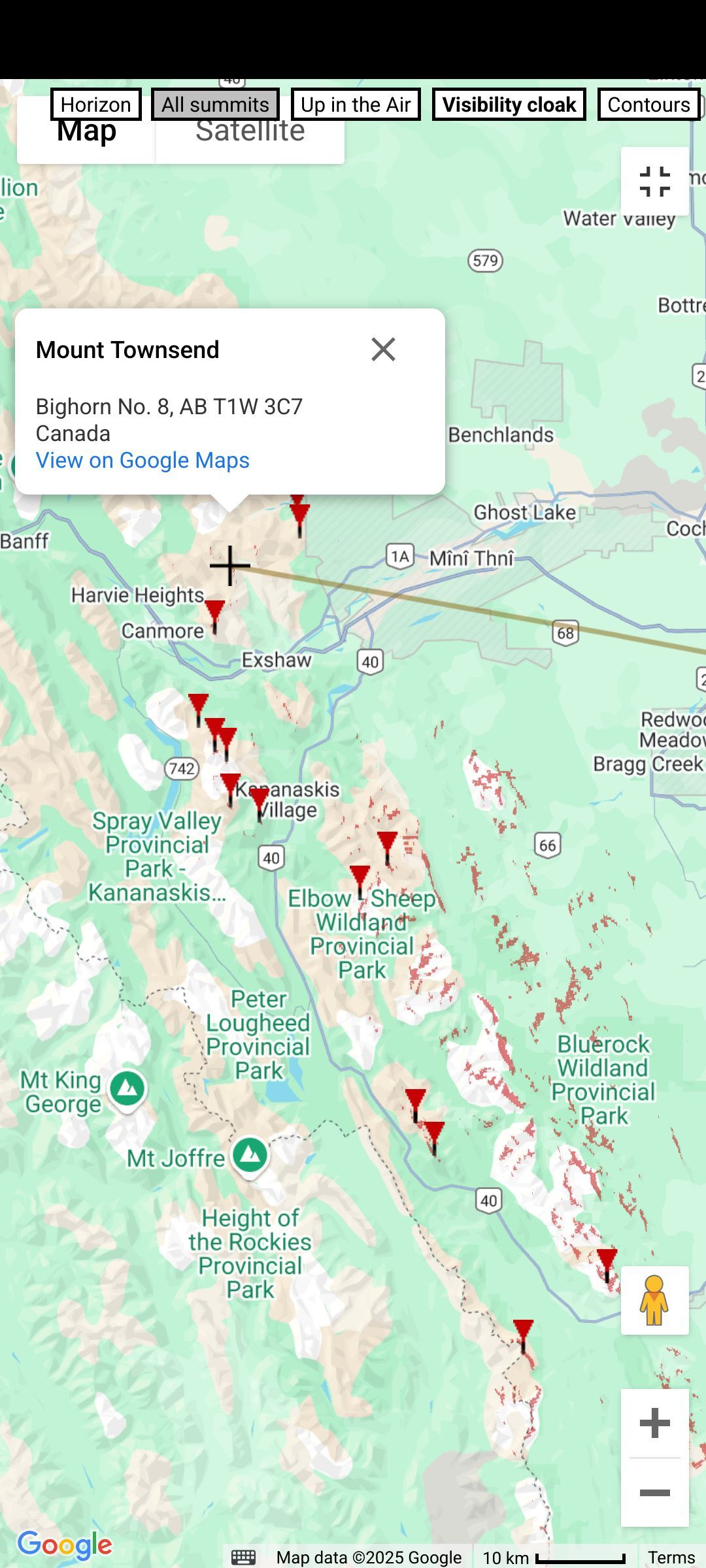
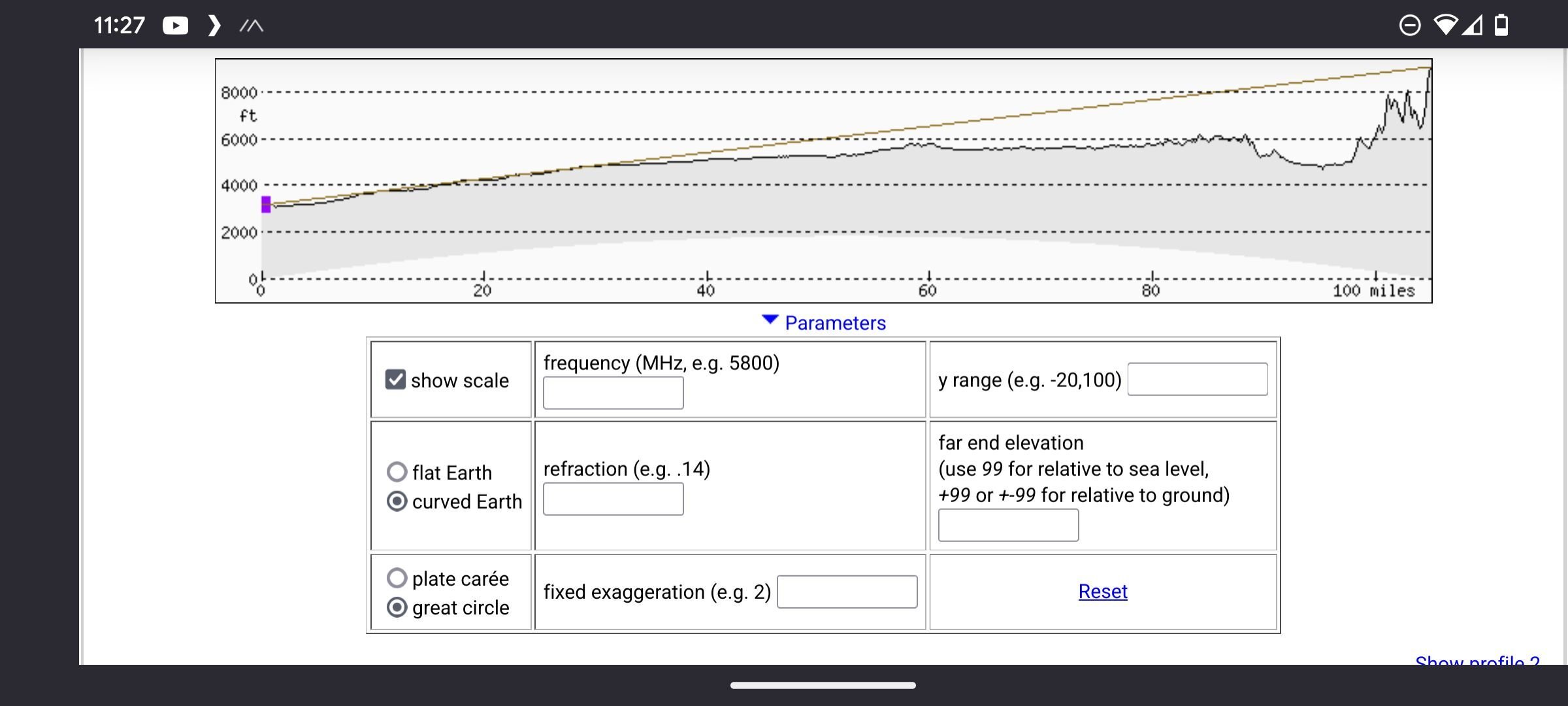
If you live somewhere where you can see a city, landmass, or landmark VERY far away (10 miles plus, ideally), then you can easily test the heliocentric globe model for yourself. (Binoculars/telescope are encouraged if you have them, so you can see even further; all that matters is that you can establish a visual.)
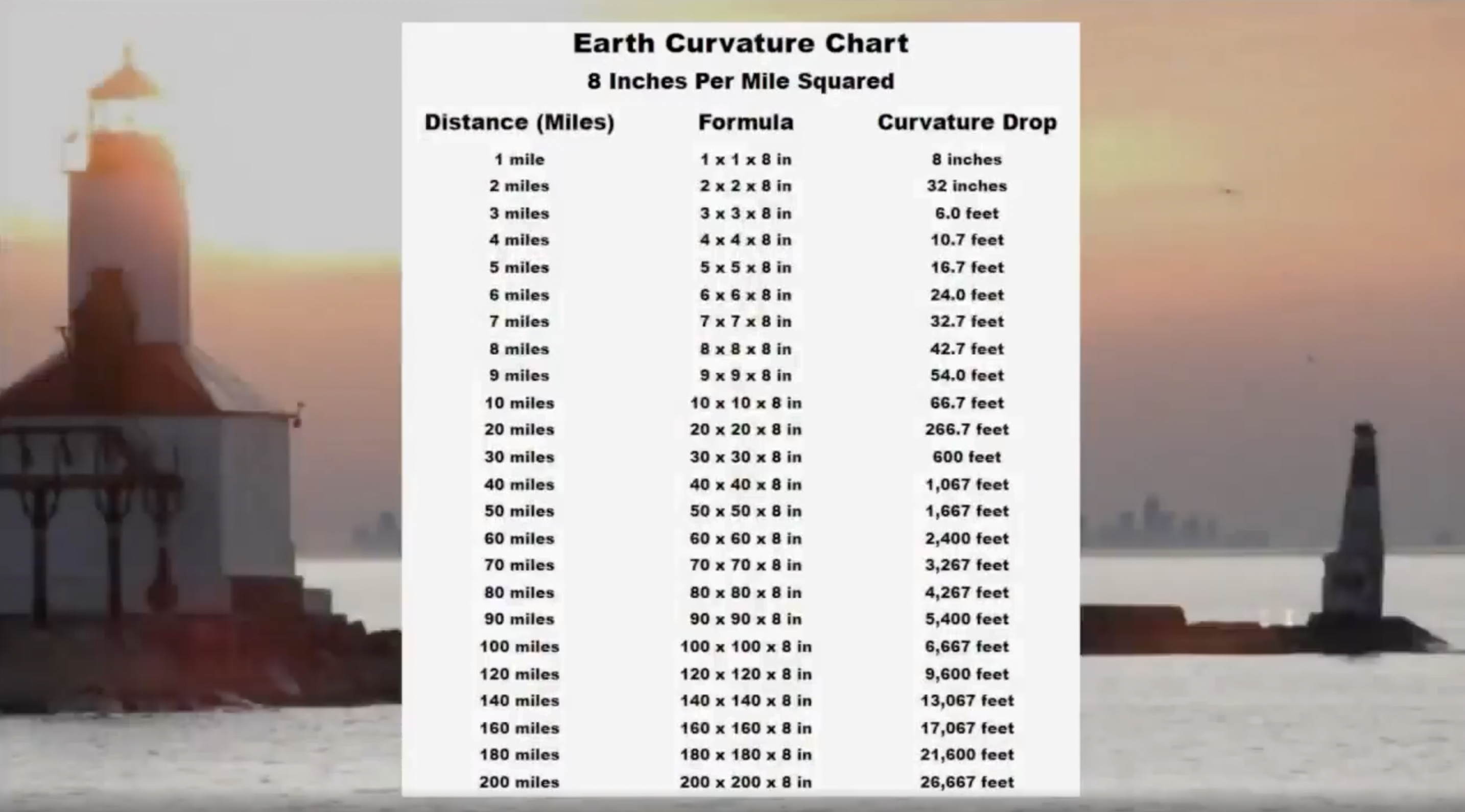
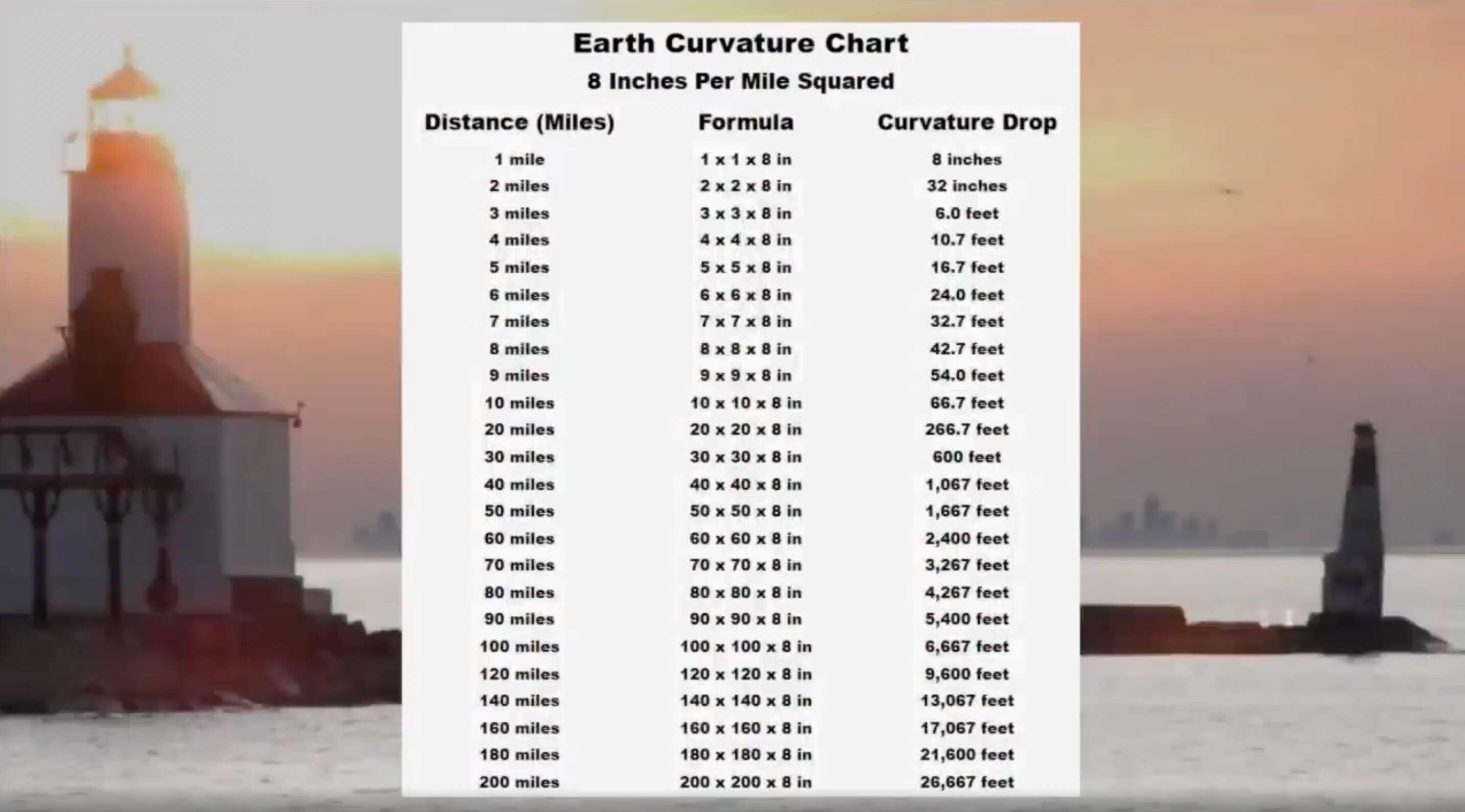
Once you've made eye contact with Location B from Location A (your location), refer to this chart for the corresponding distance of drop there should be from the curvature of the Earth, according to the official globe measurements.
Do you see the amount of drop that you should?
Report back with your findings!