Rate limiting mechanism for nostr based on time locking sats.

Actually, the more I think about it, the more edge cases come up with reusing the same token across multiple relays. At this point, I think it makes the most sense to treat tokens as single-use per relay. If a user wants to send the same event to multiple relays, they need multiple tokens.

Certainly! That should probably cover 99% of cases, so it makes perfect sense to prioritize stability over prioritization logic for now.

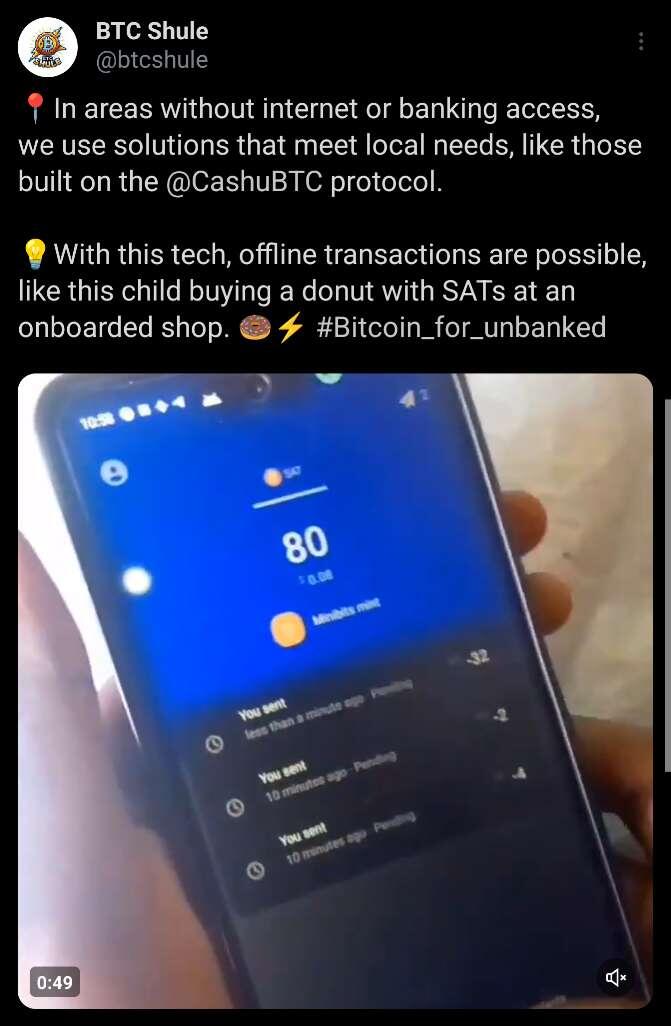
Thanks for walking me through how you deal with spam. It’s really helpful to have these real world examples to compare against my theoretical work.

Very cool! I'll read through it more thoroughly but seems like the concept (using Cashu Mints for access tokens) is adjacent to what I had in mind, minus the sat time-locking part. Thanks for chiming in!

First off, thank you so much for the reply! I'm really happy to have someone engage with the stuff I've been thinking about. As for your questions...

> do Privacy Pass tokens have value?

They don't have value in the sense that Cashu tokens have value. They are an unlinkable credential. All a Privacy Pass token encodes in this case is "this user time-locked some amount of sats for some amount of time." Tokens are short-lived and tied to a key epoch.

> are tokens accepted across relays?

I haven't quite made my mind up about this, so I thought you might have some insight into what makes the most sense for Nostr.

The simplest approach is the Issuer and Relay being the same entity. This allows the relay to stay fully offline by checking tokens against an internal spent list, whereas portability across multiple relays (where the Issuer is a separate entity) would likely require an online check to sync the tokens 'spent' state.

This isn't ideal if we want a user to be able to publish the same event to multiple relays with a single token. I have some ideas for redemption without having to contact the issuer:

1. Bind to event_id: We could choose the Nostr event_id as the secret that gets blind signed. The token is then tied to that exact event and acts as a ticket usable across multiple relays. However, this prevents batched issuance (you can't create the token until you know the event), and allows for time-correlation attacks if spent immediately after issuance.

2. Bind to Ephemeral Keys: We choose ephemeral pubkeys as the secrets. In addition to attaching the token, the user signs the event with the corresponding ephemeral privkey. No observer (e.g. a malicious relay) can reuse that token because they don't know the privkey. However, a user could theoretically use a single token to send 1,000 different events to 1,000 different relays. I'm not sure if that is a problem. What do you think?

> Do Issuers have a reputation and how do they become reputable?

Yes definitely, we need reputation if the Relay isn't the same entity as the Issuer! So a relay would most likely advertise "I only accept PP tokens from this list of Issuers I find reputable." Reputation would be built over time (sats always get unlocked on time, total token volume from the Issuer aligns with other metrics, etc.). If Cashu Mints actually end up issuing PP tokens as well, reputation could be inherited from the Mint's existing reputation. Hope I understood your question right.

> On the other hand, I think that Cashu might be the best fit for this use case

It definitely makes it a lot simpler. I just wanted to include the trust-minimized option because of how some people react to giving up their custody over sats.

> Do you imagine mints and PP token issuers being the same entity?

I think it would make sense if Cashu Mints and PP token issuers are the same entity. Of course, that's not for me to decide. If Mint operators agree that something like this would be worthwhile, then they might adopt it.

Thanks again, I really appreciate it!

> So now, we base the rate limiting on the number of requests per second that the relay can send to the rank provider. It's simpler, more effective, and users are not penalized for being behind an IP group

Nice, this should definitely make UX much better for VPN users!

I am curious though, if you hit that rate limit (say, during a spam wave), how does the relay decide which requests to prioritize? It seems like a spammer could still "crowd out" legitimate requests by jamming the queue. That is one of the key problems I'm targeting: giving the relay a way to distinguish and prioritize higher "bonded" traffic over cheap spam when resources are scarce.

> I'm curious to hear more about your approach.

Gladly! As you mentioned, traditional rate limiting is a bit lacking for permissionless, decentralized networks. IP based rate limiting penalizes privacy-conscious users (VPN/Tor), everybody hates interactive CAPTCHAs (and AI is getting better at them than humans anyway), behavioral CAPTCHAs are a privacy nightmare, and PoW discriminates against mobile devices. Paying for events (e.g., proof-of-burn, Thomas Voegtlin) definitely works, but I worry it creates too high a UX hurdle for widespread adoption.

What I'm proposing is an economic, privacy-preserving mechanism that works by time-locking sats instead of burning them. Ideally, this has near-zero cost for legitimate users (minus opportunity costs and routing fees), whereas spammers must immobilize capital proportional to the event throughput they want to sustain.

For example, a normal user might lock a trivial amount (e.g. $10) to generate enough tokens for a full day of activity. In contrast, capital requirements scale linearly for spammers. To sustain 10,000 requests/sec, an attacker hits a massive liquidity wall, effectively needing to lock millions of dollars just to keep the attack running. Crucially, relays can also dynamically adjust the lock requirement based on load (like 'surge pricing'). While this slightly increases the bond for honest users, it forces the attacker’s capital requirements to scale more than linearly.

The mechanism works by requiring events to include Privacy Pass tokens. These work very similarly to Cashu tokens: Users go to an Attester/Issuer (the Mint) with blinded secrets, perform an action (locking sats), and get signed secrets in return. The user unblinds them to get a batch of tokens, which they attach to events. This allows the Relay to verify the sats were locked without them or the Mint being able to link the event back to the locking transaction.

> Are you basing your solution on something like Cashu, or just LN with hold invoices?

Yes, those are the two options I have in mind.

1. Cashu: Users lock ecash. Cashu Mints are well positioned to issue Privacy Pass tokens as well, but users run the risk of the Mint rugging their funds.

2. LN Hold Invoices: This is more trust-minimized. I "tweaked" the standard flow so that the sender chooses the preimage that unlocks the hold invoice (rather than the receiver/Mint). This ensures the Mint cannot possibly settle the invoice and rug the user.

The issue with the Hold Invoice approach is that, because the invoice never gets settled, routing nodes don't get compensated for the locked liquidity. So this likely requires upfront/holding fees for the routing nodes (no longer near-zero cost) or a direct channel from User to Mint.

That's the gist of my idea! I'm currently writing my Master's thesis on this, so I'm really looking for feedback from people actually dealing with these constraints in production. Since my applied crypto group at university doesn't focus heavily on Bitcoin, I've unfortunately had very limited input from experts in LN/cashu/nostr so far. I'd absolutely love any thoughts you have, or if you know anyone else who might be interested, that would be incredibly helpful.

"We've also replaced IP-based rate limiting for rank lookups with an approach that no longer penalizes users behind VPNs, and improved response handling to be more robust under real-world conditions."

Very curious about how this works. Mind sharing more?

I'm also working on a rate limiting mechanism for nostr where users have to time lock sats in order to make requests (based on Privacy Pass). It's for my master thesis, so I'd love to compare it to whatever you're using. Thanks!

Apologies for sending the unsolicited pdf, if that was the issue.

Privacy Pass for rate limiting (on nostr) is actually exactly what I'm working on in my master's thesis. Thanks for the words of encouragement some months back, btw!

While I find Thomas Voegtlin's Proof-of-Burn proposal interesting, I worry that burning sats for every event creates too high of a UX hurdle for widespread adoption.

My idea was that instead of burning sats, Clients have to time lock them in order to receive Privacy Pass tokens. A legit user incurs near-zero costs for normal usage, whereas spammers must immobilize capital proportional to the number of events they want to sustain, capping their throughput based on their available liquidity.

I would love to share more with you if you have the time. I'd really value feedback from people deep into this stuff, as my university lab focuses less on Bitcoin specifically.

Very nice work!

Though I do worry that having to burn sats for every event will be too big of a UX hurdle to gain widespread adoption.

That's why I've been working on a spam deterrent where users have to time lock sats instead of actually having to spend them. A legit user incurs near-zero costs, whereas attackers must immobilize capital proportional to the number and lifetime of identities they maintain. If you, or anyone reading this, is interested, check out my latest post. I'd love feedback from the community!

Still, proof-of-burn is very interesting and might be needed as the ultimate deterrent at some point. Thanks for writing the paper!

"Don't think I like deliberately burning the money", "Maybe better, but still makes messages mostly for the rich?"

100% agreed. That's why I'm trying to create a spam deterrent that works by time locking sats, not actually spending then. While proof-of-burn is really interesting and would definitely be a strong deterrent, I do worry the UX hurdle of having to spend sats for every little action might be too high to gain widespread adoption.

If you, or anyone reading this, is interested, check out my latest post. I'm desperately looking for feedback from the community!

"I can cryprographically prove that I'm human"

Are you talking about WoT here? Would love to know!

I'm trying to tackle the problem of bots being everywhere while legit users still have to deal with annoying counter measures (e.g. CAPTCHAS) in my master's thesis. The idea is to time lock sats to get tokens that can then be spend to access web resources. A legit user incurs near-zero costs, whereas attackers must immobilize capital proportional to the number and lifetime of identities they maintain.

See my latest post if anyone's interested. I'm desperately looking for feedback from the community 😅

"Time locked sats as sybil/spam protection"

If this sounds interesting to anyone, I'd love to share the whole draft with you. I'm desperately looking for feedback! 😅

Just realized that for the 'Blank Check' approach to work, we have to make sure that only a single party has access to a specific set of blank checks.

Otherwise, we run the risk that a check gets used twice but Carol can only redeem it once.

If we have to restrict access to the checks, that probably defeats the original purpose: 'An offline receiver could publish their public key and the online sender can prepare a suitable BlindSignature from the mint.'

Oh yes, this is the attack I meant.

"She can *spend* it later when she is back online" not "unblind".

I don't think *this* is a problem. If Alice and the Mint collude they can always unblind C_, so this isn't really a downgrade from standard cashu.

However, there is an attack where Alice just lets the Mint sign Y twice. Once with Carol's public key B_ = Y + r * F and once the standard way with B_' = Y + rG.

Now, (x, r_, C_, DLEQ) looks like a valid token to Carol even when offline. However if Alice spends her token before Carol, Carol's token will get denied because the secret x is already in the Mint's spent set.

An idea to fix this:

1. Carol generates a bunch of secrets x, blinds them (B=Y+rG), and publishes these "Blank Checks" (B_'s) somewhere. She can then go offline.

2. Alice grabs a B_, pays the Mint to sign it (C_), and sends it to Carol. Alice cannot have Y signed twice (like in the prior attack) because she doesn't know x.

3. Carol receives C_ and the DLEQ proof. She verifies the proof against her original blank checks and the Mint's public key. If one of them passes, she has cryptographic proof that C_ is the valid signature for her specific B_. Since only she holds the secret x, she knows the token is safe and unspent. She can unblind it later when she is back online.

Not sure if I'm making any mistakes or the first step defies the purpose you want to use this for. I'm pretty new to all of this myself. Would love to hear what you think!

Still would love to collaborate!

Gotcha! Thanks.

Yeah that does in fact sound like a mistake 😂Canned 'Krombacher' from Aldi will always remind me of my days at university so it has a special place in my heart but there sure are much better beers out there

Tell me about it... Writing my master thesis at the applied cryptography lab just because I really enjoy btc/LN/cashu might not be the way to go 😅

Which one?

Hope you don't mind me asking but shouldn't NUT-12 be mandatory, because without the DLEQ proofs a mint could theoretically tag every minted token with its own private key? As far as I understand it, this could then be used to recognise the tokens once they eventually get redeemed?

I could definitely be off, just trying to understand it better. Thanks for all the great work you do, very inspiring!

Amazing! This is thanks to NUT-12, correct?