I wish I had that kind of pencil 😆
I would contribute more but my life is currently very complicated 😬
Anyway. Stay lurky 💪
Obviously without entering the passphrase you still can access the funds, if that wasn't clear already 😉
I'm pretty sure every passphrase acts as an additional seed word. Therefore completely different derived key.
So nr1: a new empty account is accessed
Would it be possible to have optional "nsec aliases"?
For example I have 3 nsecs on nostr for different use cases or "other stuff".
Now I want to merge or connect 2 of those nsecs with my main nsec.
The result: different nsecs merged with one profile or alias.
Some time later I learn one of those nsecs gets compromised - I disconnect (or revoke) this nsec from main nsec and live on happily as if nothing happened
#asknostr #newfeature
A ratchet can only turn in one direction.
The double ratchet means two types of ratchets: a KDF ratchet (the small ratchet in the diagram) and a DH ratchet (the large ratchet in the diagram).
KDF stands for Key Derivation Function. A hash function is the simplest KDF because it is one-way. K1=hash(K0), K2=hash(K1), K3=hash(K2), K4=hash(K3)... K1 is used to encrypt the first message, K2 to encrypt the second message, and so on. Once used, the key is deleted. If an attacker obtains the latest encryption key K5, they cannot reverse-engineer K4, K3, K2, or K1, ensuring the security of historical messages. Thus, the KDF provides forward secrecy to the encryption protocol.
However, the attacker can derive K6, K7, K8..., which means there is no backward secrecy. This is where the DH ratchet comes into play.
The Diffie–Hellman (DH) key exchange is a mathematical method for securely exchanging cryptographic keys over a public channel. Alice, using her private key S1 and Bob’s public key P2, can compute a value. Similarly, Bob, using his private key S2 and Alice’s public key P1, can compute a value. These two values are equal.
Alice and Bob continuously generate new DH key pairs for new messages on the client side and attach the public key in plaintext to the message. The message recipient can then use this public key and their private key to perform the DH computation. This DH ratchet effectively resets the KDF ratchet with the DH ratchet. Because the attacker does not know the latest DH private key, they cannot derive future encryption keys, thus providing backward secrecy.
Therefore, in the double ratchet algorithm, the KDF ratchet ensures forward secrecy, and the DH ratchet ensures backward secrecy, together achieving both forward and backward secrecy.
We recommend the following video, which provides a more intuitive animation demonstration.
https://youtu.be/9sO2qdTci-s?si=BXLU33BRANWAJKMz
https://youtu.be/7uEeE3TUqmU?si=jpPOR_O61IppgJxl
(We hope users can understand the basic principles to judge for themselves which chat applications are good.)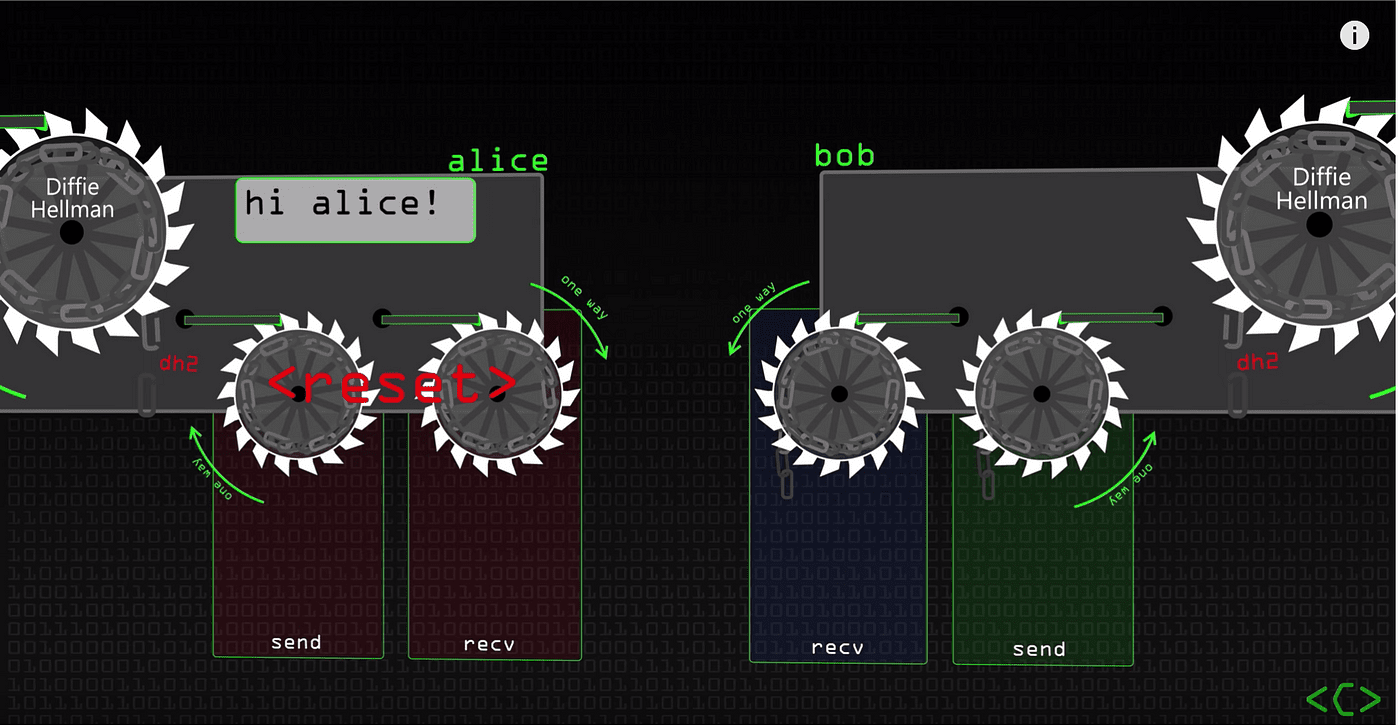 
nostr:note1ffgsgvkltl96wzwe6lakv2ntjfkq2u48msx57mrvnnhtyde5s2js8antlr
Nice, finally I understand the underlying process.
Happy Mother’s Day, nostr:npub1hu3hdctm5nkzd8gslnyedfr5ddz3z547jqcl5j88g4fame2jd08qh6h8nh
Our son has no idea how outrageously cool his mom is… he really hit the jackpot (as did I 🧡). 
Such a lovely picture
Neat!
How do you paint PETG?
Seems like I caught this thing blasting the magnetosphere:
Hey, all you northerners in middle latitudes: Go out tonight and check if you can see an Aurora.
I actually did for a few minutes in southern Germany 🤩🤯
I have questions 😵
Because Taxes. As always
Why have you changed the direction of the arrows? Why Counter-Clockwise?
Are you a madman?!!?
